光谱去噪和基线校正和特征提取算法在光谱分析中具有至关重要的作用,其重要性主要体现在以下几个方面:
一、提高光谱质量:在实际测量中,光谱信号常常受到各种噪声和干扰的影响,导致信号质量下降。光谱去噪和基线校正算法能够有效地去除噪声和干扰,还原真实的信号特征,提高光谱数据的可靠性和准确性。这对于后续的数据处理、分析和物质成分识别至关重要。
二、增强谱图可比性:基线校正能够消除由于仪器、实验条件等因素引起的谱图差异,使得不同时间、不同实验条件下获得的谱图更具可比性。这对于实验结果的一致性和可重复性至关重要,有助于推动科学研究和技术创新。
三、 提高分析精度:通过有效的去噪和基线校正,可以更准确地提取光谱特征,从而提高物质成分的定性和定量分析精度。这对于化学、生物医学、环境监测等领域的质量控制、疾病诊断和治疗以及物质成分的深入分析具有重要意义。
四、降低计算成本:在处理大规模数据集时,光谱提取特征算法能够有效地降低数据的维度和复杂性,减少计算资源和时间的消耗,提高计算效率。这有助于加速数据处理和分析过程,降低计算成本,提高工作效率。
五、
1、光谱平滑去噪
MG光谱平滑去噪是一种在光谱分析中常用的去噪方法。它结合了MG平滑滤波和光谱分析的原理,通过在光谱数据上应用平滑滤波器,去除噪声,提高数据质量。在MG光谱平滑去噪中,首先需要对光谱数据进行预处理,包括对数据进行归一化、标准化等操作,以消除数据间的差异和异常值。平滑滤波器通过计算邻近像素或波长的平均值或加权平均值,去除噪声和细节,使数据更加平滑。
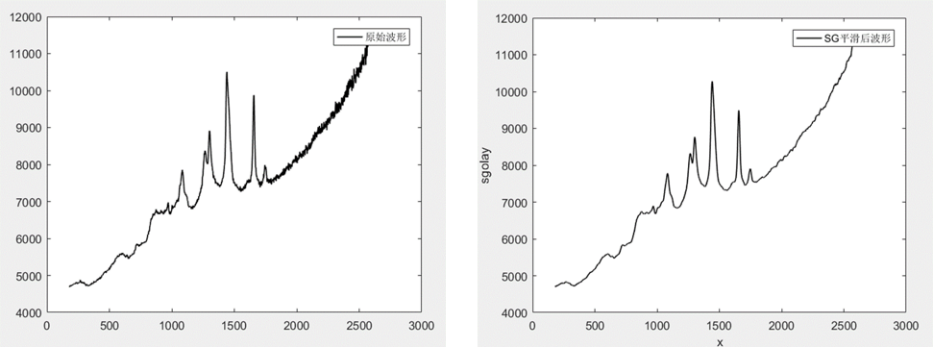
基于MG的光谱平滑去噪
2、迭代自适应加权惩罚最小二乘法(airPLS)实现光谱基线校正
在迭代加权最小二乘法中,每次迭代都会根据目标函数的当前估计值来更新权重。如果某个数据点对目标函数的贡献较大,那么在下一次迭代中,它将被赋予更大的权重;反之,如果某个数据点对目标函数的贡献较小,那么在下一次迭代中,它将被赋予更小的权重。然而,迭代加权最小二乘法并不能很好地处理数据中存在多个局部最优解的情况。为了解决这个问题,迭代自适应加权惩罚最小二乘法被提出。迭代自适应加权惩罚最小二乘法在迭代加权最小二乘法的基础上引入了一个惩罚项。这个惩罚项的作用是鼓励目标函数在迭代过程中向全局最优解靠近。具体来说,每次迭代都会根据目标函数的当前估计值和已知的数据来计算一个惩罚项,并将其加到目标函数中。这样,在每次迭代中,不仅考虑了数据点到当前估计值的距离,还考虑了数据点到全局最优解的距离。
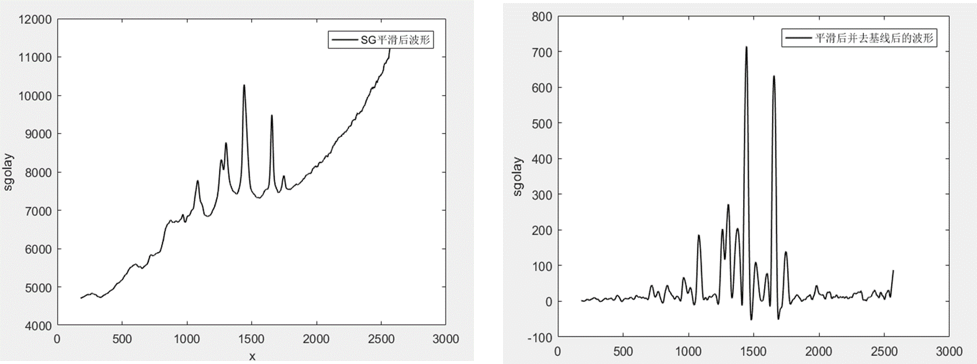
基于airPLS的光谱基线校正
3、小波变化提取光谱峰位
小波变换是一种信号处理方法,它可以将信号分解为不同尺度的成分。在光谱分析中,小波变换可以用于提取光谱数据的局部特征,如峰位、谷位等。通过寻找不同尺度的小波系数中的极大值点,可以确定光谱数据中的峰位位置。首先对光谱数据进行小波变换,将原始光谱数据分解为不同尺度的小波系数。然后在不同尺度的小波系数中,寻找对应于峰位的局部极大值点。这些极大值点对应于光谱数据中的峰位。最后根据极大值点所在的位置,确定峰位的坐标。
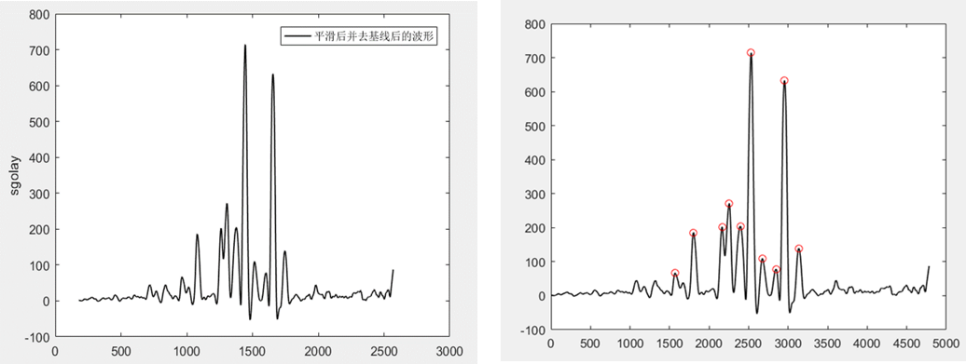
综上所述,光谱去噪和基线校正算法在提高光谱质量、增强谱图可比性、提高分析精度、降低计算成本等方面具有举足轻重的地位。随着科学技术的发展,这种算法的重要性和应用价值将会进一步凸显。
文字报道:洪岩
文章编辑:董荣录